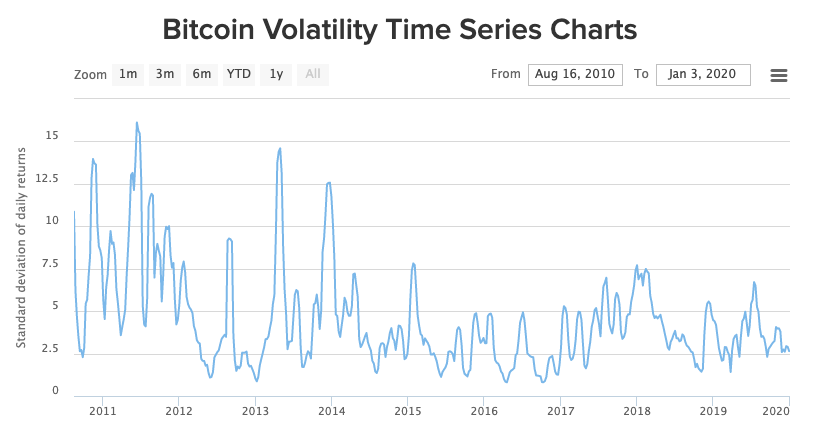
Epistemic status: just trying to understand the Bitcoin whitepaper. The first 12 headings correspond to the parts in the whitepaper. My investment advice would be to invent a time machine to beat Satoshi. Eliezer Yudkowsky on Bitcoin as Pascal’s mugging: if you can’t manage to not regret having not bought Bitcoin even though you knew about it when it was $1, you shouldn’t ever buy anything except index funds because you are not psychologically suited to survive investing.
Inspired by Ben Reinhardt’s Seminal Paper Club, I wanted to read more seminal papers starting with Satoshi Nakamoto’s Bitcoin whitepaper Bitcoin: A Peer-to-Peer Electronic Cash System. It’s surprisingly short (9 pages) and readable, definitely recommended.
Bitcoin is a clever but ugly solution to the double-spending problem using a peer-to-peer distributed timestamp server to generate computational proof of the chronological order of transactions. While Bitcoin is far from the first attempt at electronic money, and in fact involves no major mathematical or cryptographic breakthroughs, it has become a Schelling point synonymous with cryptocurrency, and remains by far the largest one by market capitalization and trading volume.
Key dates:
- 05/2007: coding began in C++
- 08/2008: domain name “bitcoin.org” registered and feedback on drafts of the whitepaper was sought from Wei Dai and Hal Finney
- 31/10/2008: the whitepaper was published to a public cryptography mailing list
- 03/01/2009: open-sourced and launched the Bitcoin network with the mining of the genesis block
- 12/01/2009: first Bitcoin transaction of 10 BTC from Satoshi to Finney
- 05/2010: first commercial Bitcoin transaction of two Papa John’s pizza for 10,000 BTC (288,755,000 USD as of 2020/12/31)
- 04/11: control of Bitcoin website and repository was handed off to Gavin Andresen (600,000-700,000 BTC still sits at Satoshi’s address today)
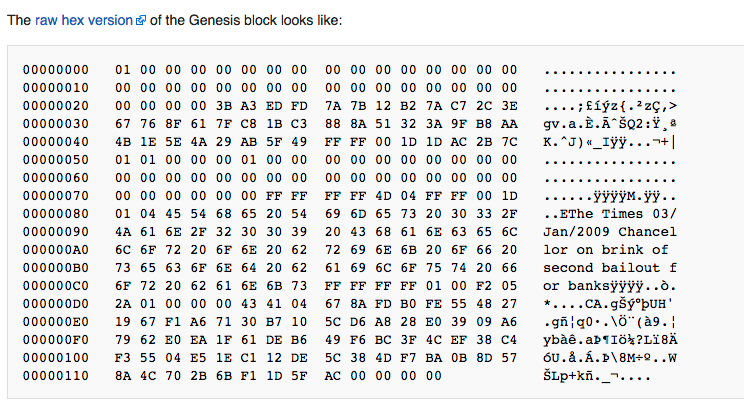
Embedded in the coinbase was “The Times 03/Jan/2009 Chancellor on brink of second bailout for banks.” A comment on the instability caused by fractional-reserve banking as seen in quantitative easing since the 2008 Financial Crisis.
- Introduction
- Transactions
- Timestamp server
- Proof-of-work
- Network
- Incentive
- Reclaiming Disk Space Using Merkle Tree
- Simplified Payment Verification
- Combining And Splitting Value
- Privacy
- Calculations
- References
- More Nice Graphs
- Additional reading
Introduction
Satoshi begins by pointing out the inherent weaknesses of relying almost exclusively on financial institutions to serve as trusted third parties to process electronic payments. Transactions can be reversed when banks mediate disputes, which increases transactional cost, limits minimum practical transaction size, and providers non-reversible services risk not getting paid. Third parties are:
- untrustworthy;
- frequently hacked;
- give too much information to the government without consent;
- and accept a certain percentage of fraud as unavoidable thus increasing everyone’s cost.
Bitcoin replaces trust with cryptographic proof by allowing any 2 willing parties to transact directly with each other without the need for a trusted third party.
As William Stanley Jevons famously defined in Money and the Mechanism of Exchange, the properties of money are:
- store of value i.e. non-perishable and consistently valued by others;
- medium of exchange;
- and unit of account.
Anything can serve as money as long as there is stable social consensus about its value i.e. trust.
Though the overwhelming majority of bitcoin transactions take place on a cryptocurrency exchange, rather than being used in transactions with merchants. Delays processing payments through the blockchain of about ten minutes make bitcoin use very difficult in a retail setting. But hey, Sci-Hub runs on Bitcoin donations!
Transactions
Cryptographic proof
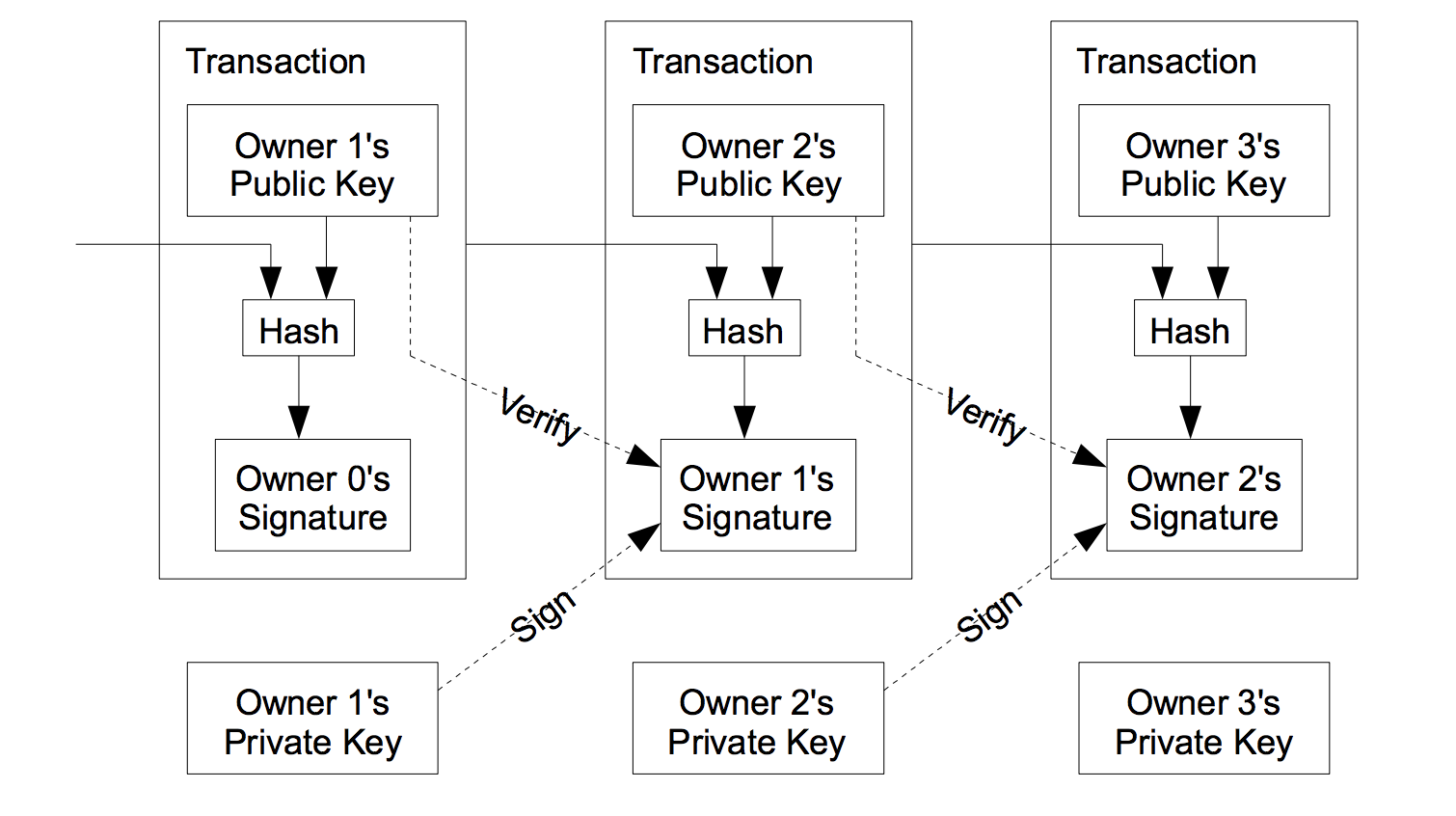
Satoshi defines an electronic coin as a chain of digital signatures. A digital signature is where the public-key encrypts plaintext, and the private-key deciphers the ciphertext. In Bitcoin, your key pair is itself your identity, hence the pseudonymity. A digital signature can be expressed as:
- Sign(message, KEYprivate) = 256-bit signature
- Verify(message, 256-bit signature, KEYpublic) = T/F
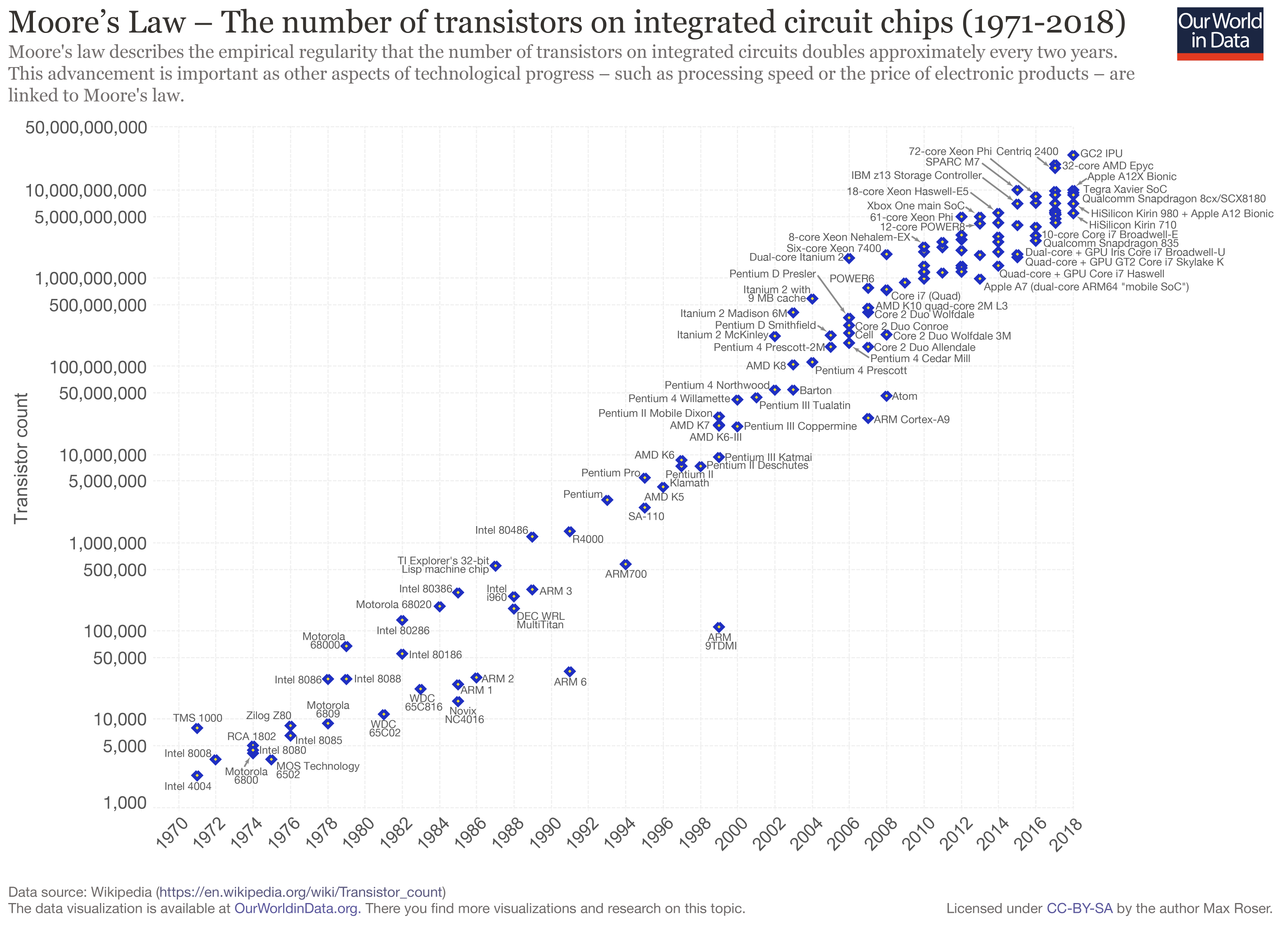
Of course, it is a bit more complicated in practice. Public-key cryptography began when the RSA (Rivest–Shamir–Adleman) cryptosystem was invented in 1977 from the trapdoor function (functions that are harder to compute than to verify) of integer factoring. For instance, it is harder to find the prime factors of 177 but easier to verify the multiple of 3*59. RSA key size has ballooned to the current recommendation of 2048 bits to compensate for Moore’s Law.
Almost all cryptocurrency deploys Elliptic Curve Digital Signature Algorithm (ECDSA), and Bitcoin popularised using secp256k1. It is a type of elliptic-curve cryptography (ECC) which is built out of the trapdoor function of multiplying over elliptic curves in finite fields. Our best algorithms for computing discrete logarithms over certain elliptic curves are exponential, while our best algorithms for factoring integers are sub-exponential, hence integer factoring is easier (though not all curves are the same). Standard ECC keys are 256 bits, about 1/10 the size of RCA keys, and collision-resistant i.e. two inputs do not hash to the same output.
The security of an encryption scheme is established by a reduction i.e. a proof that if this scheme is broken, another known hard problem can also be solved. If reduction is not enough, security is likely to be proportional to the number of mathematicians who failed at solving it! Because P vs NP is still unsolved, it is an open question whether integer factoring and computing discrete logarithms are truly hard NP-complete problems i.e. no algorithm can solve in faster than in exponential time (e.g. computing perfect strategy in chess). However, Shor’s algorithm can efficiently compute discrete logarithms on a quantum computer. Luckily, a Bitcoin address is the 160-bit hash of a 256 bit public-key for compression, which provides quantum resistance; a quantum computer can only be quadratically more efficient, so there is still 80-bit security.
Public-key cryptography is a kind of asymmetric encryption, as compared to symmetric encryption that uses the same key for both encryption and decryption. As it happens, the former is much slower (measured in milliseconds i.e. 10-3 s) than the latter (measured in microseconds i.e. 10-6 s). Hence, protocols generally use asymmetric cryptography to establish identities, then create a shared session key to continue communicating over a symmetric cipher.
Any public-key cryptography system depends on robust key generation, and turns out computers are deterministic machines that don’t always generate high-quality randomness! Insufficient entropy in key generation has led to many attacks against cryptosystems, for example a bug in Android led to many Bitcon apps generating insecure private keys that were quickly cracked. This is why in practice people always say never roll your own crypto.
Double-spending problem
Satoshi raises the main problem that Bitcoin solves: double-spending. Alice can pay the same digital $10 to Bob and Charlie, neither of whom can tell which copy is real. PayPal’s anti-counterfeit effort involved a single database with no direct user access, but Cypherpunks tried to solve the double spend problem without having to trust a third party. For example, e-gold was collateralised with gold, while DigiCash was collateralised with USD, but neither was beyond state control. b-money by Wei Dai and BitGold by Nick Szabo were proposed schemes vulnerable to sybil attacks where a botnet can determine the outcome of a majority vote.
Timestamp server
If Alice sends double-spend by sending Bitcoin to Bob and Charlie, Bob can verify that it is indeed from Alice using Alice’s public-key, but so can Charlie. To solve the double-spending problem without relying on third-party minting, all transactions must be public and every participant must adhere to a single history of transactions to determine which transaction was received first.
Satoshi proposes a timestamp server as a form of public ledger. It is a series of (hash, timestamp) where it calculates the hash of a block of previous timestamps and publishes it widely.
Proof-of-work
A cryptographic hash function inputs a string of characters of arbitrary length and maps it to another string of characters of fixed length, for example SHA-256(message) = 32 byte hash. Hash functions have a few important properties:
- Deterministic: the same message always results in the same hash
- One-way: generating the message from the hash can only be brute-forced
- Avalanche-effect: changing a single bit (severely) jumbles other bits i.e. similar inputs have outputs with no discernible relationship
- Collision-resistant: i.e. two inputs do not hash to the same output
- SHA-256 has a range of 2256 while number of atoms in the universe is around 2260 so it is very unlikely to produce hash collision by pigeonholing
Trouble is that for any hash function you can actually always do better than brute-force by using a birthday attack: how many guests need to be at a party on average so two guests share the same birthday? Surprisingly, you only need 23 guests, as it gives 253 unique pairs (n(n-1))/2, each having a 1/365 chance of sharing a birthday, i.e. 50.7% chance. Hence √n is a good approximation for the 50% threshold for a birthday collision. Current computational tractability is around 280, so a SHA-128 can be birthday-attacked by brute-forcing 264. This is why if we want 128-bit security, we need a 256-bit hash function.
In a proof of work (PoW) you usually have a challenge string c and you are looking for a nonce (short for “number only used once”) n such that hash(c+n) will result in a string with a certain number of leading zeroes. Let’s say our challenge string was “Hello, world!” and our target was to get a SHA-256 hash beginning with ‘000’. One way to go about it is to start with a nonce of ‘0’ and progressively increment it until you get a hash starting with ‘000’. In this case that would take 4251 tries. If the hash is required to start with 30 zeros, the probability is 1/230 about 1 in a billion.
The only way to produce a satisfactory nonce is by guessing a lot of times i.e. spending a lot of computational power. Once the PoW is done it can be verified easily by hashing the block containing the nonce. A block also contains the list of all previous transactions, and the previous hash thus chaining to the previous block, so changing a block would change the hash of the block and all subsequent blocks, requiring all the PoW to be redone.
Thus, trust is placed at the longest blockchain which has the greatest PoW computational power invested. Users keep their own copy of the longest blockchain that has the addition of the new block from miners, producing a decentralised consensus.
A scammer has to add blocks faster to maintain the longest blockchain forever than all honest nodes adding to the blockchain, which becomes harder exponentially as the blockchain grows. As long as the majority of CPU power is controlled by honest nodes, it is infeasible for the slower attacker to catch up to the longest blockchain. To compensate for Moore’s Law and the number of miners, the number of zeroes required in the hash is increased periodically to maintain about 10 mins to find the nonce to add a new block.
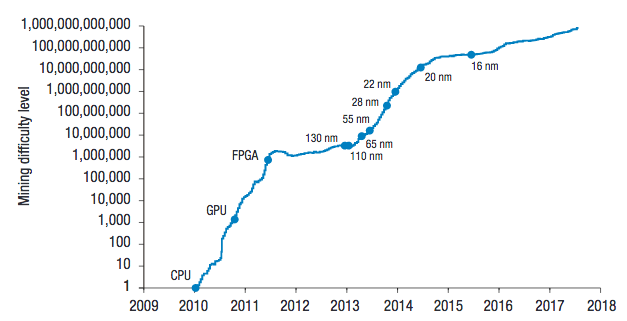
Semi-log plot of relative mining difficulty.
Unfortunately, centralised crypto mining is a growing problem as those with enough money in areas that subsidise electricity are concentrating computing power in the hands of a few.
Network
Satoshi proposes 6 steps to run the network:
- New transactions are broadcast to all nodes
- Each node collects new transactions into a block
- Each node works on finding a difficult proof-of-work for its block
- When a node finds a proof-of-work, it broadcasts the block to all nodes
- Nodes accept the block only if all transactions in it are valid and not already spent
- Nodes express their acceptance of the block by working on creating the next block in the chain, using the hash of the accepted block as the previous hash
P2P Network
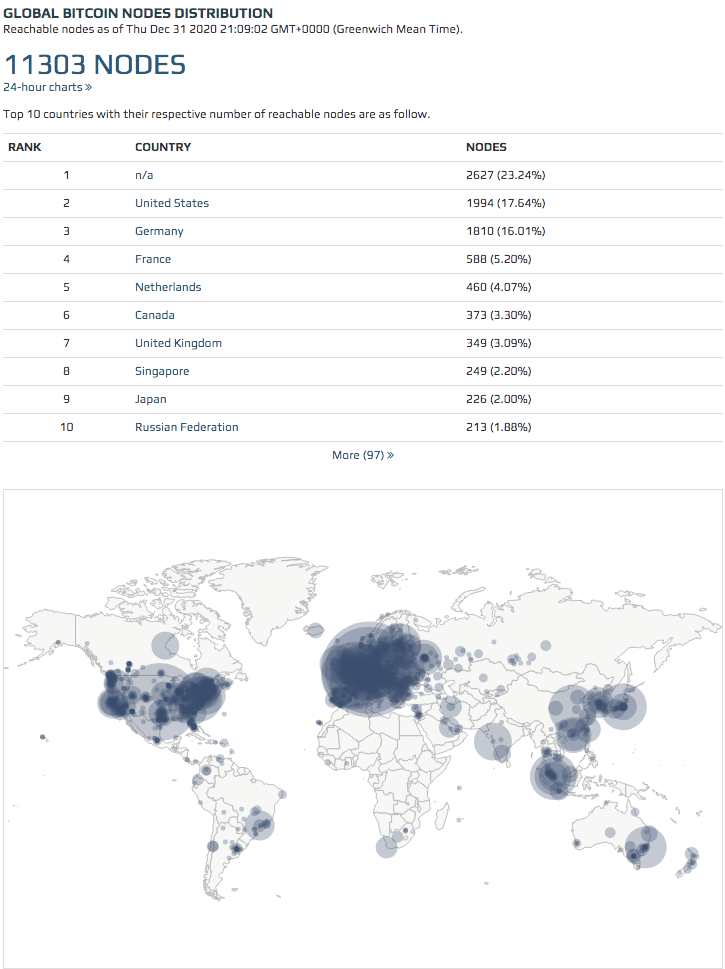
Before Bitcoin, decentralised peer-to-peer (P2P) networking was pioneered by Napster in 1999 which was a cross between client-server and P2P network: client query search is indexed at Napster server, while the file is fetched directly from peers. By 2009, BitTorrent accounted for 70% (!) of all internet traffic.
In a P2P network, each peer makes queries and responds to queries. In contrast, in a centralised client-server model, the central server or a fleet of servers behind a load balancer provides a service per each clients’ query.
In the Bitcoin P2P network, the bootstrap node is the entry point, from which point you can then organically find new peers. Of course, the danger with a bootstrap node is that if it is not authenticated, it could be malicious and perform a man-in-the-middle or eclipse attack. In Bitcoin Core, the canonical Bitcoin implementation, these bootstrap nodes are hard-coded as trusted DNS servers maintained by the core developers.
Pros of P2P:
- Crash fault tolerant: even if individual nodes fails, the system functions, which is crucial to scalability
- Censorship resistant: even if individual node is censored, the network is not censored
Cons of P2P:
- A coherent single snapshot of the global state only possible in centralised architecture
- High churn rate when peers go online and offline means demanding high fault tolerance
- Hard to moderate and cannot enforce quality control (Bitcoin uses a reputation system where infractions score points, and enough points result in shadowbans)
- Lack of network-level privacy (pseudonymity provides some privacy, but if you connect to just 50% of the network, you can see the “message wave” propagate from the sender and figure out their IP address)
Since 2015, Bitcoin has used diffusion to propagate gossip messages, where the client waits a random exponential delay before gossiping to its peers. It can be written as:
def gossip(msg):
for peer in peers:
schedule_send(peer, msg, wait=np.random.exponential(1.0 / theta))
Unfortunately, there is still a lot to be done to improve Bitcoin’s network-level privacy,
Incentive
Creating a block by doing the PoW i.e. mining, is rewarded with a small amount of Bitcoin in a special transaction called a coinbase, thus introducing new bits of Bitcoin to the economy. Each block is limited to around 2,400 transactions, compared to Visa handling on average 1,700 transactions/second and up to 24,000 transactions/second (which is known as the Bitcoin scalability problem). To incentivise miners to include Alice’s payment to Bob in a block, Alice can optionally include a transaction fee for the miner, which also incentivises attackers to choose putting computational power to mining over scamming.
Every 210,000 blocks, around 4 years, the reward for PoW is halved. As the reward decreases geometrically over time, it creates an artificial scarcity as there will never be more than 21 million Bitcoin. The limit will be reached circa 2140, and further proof of work to continue the blockchain will be rewarded solely by transaction fees.
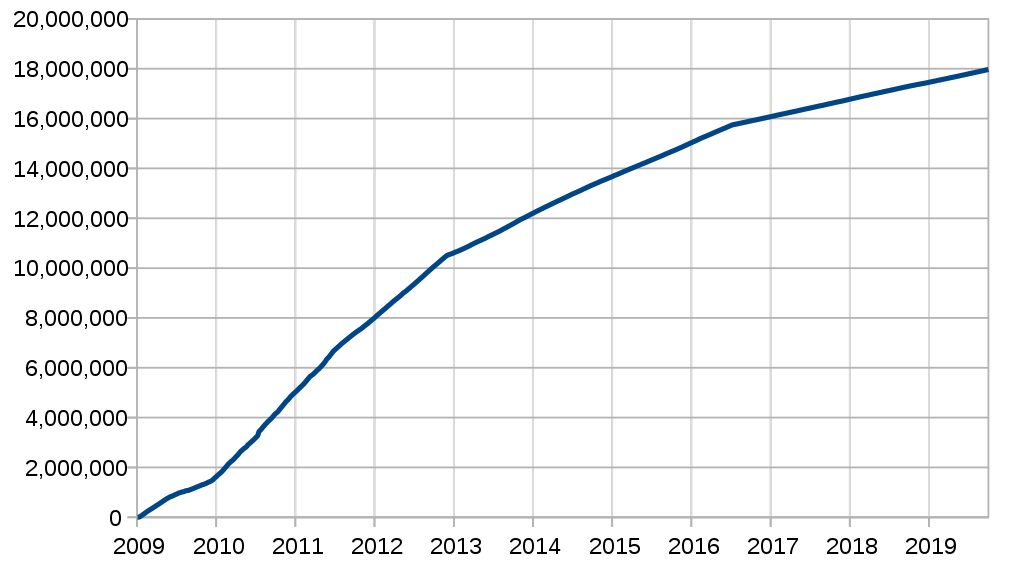 Total Bitcoins in circulation.
Total Bitcoins in circulation.
Mining Bitcoin gets progressively harder as the network grows, and so eventually mining it en masse requires a lot of hardware, electricity, and cooling. This creates a breakeven point for mining, which is a factor that was not anticipated by Satoshi.
Reclaiming Disk Space Using Merkle Tree
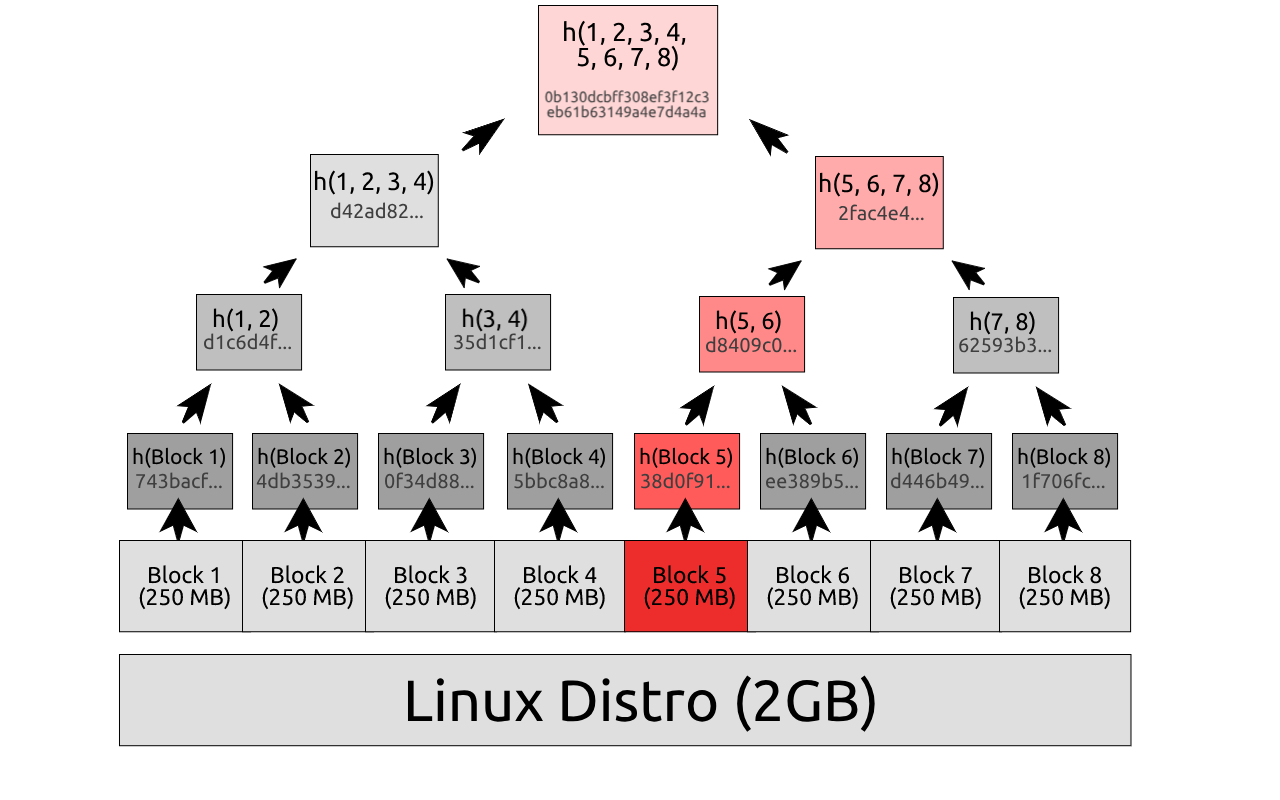
A Merkle tree is what you get when you repeatedly hash (e.g. SHA-2) pairs of nodes until there is one hash left. If the number of transactions is odd, the last hash will be duplicated before hashing. You can create a hash tree with only 2 elements:
from hashlib import sha1
def h(s): return sha1(s.encode()).hexdigest() # hashing helper function
block1 = “Block 1”
block2 = “Block 2”
digest1 = h(block1)
digest2 = h(block2)
root = h(digest1 + digest2)
print(root)
# d1c6d4f28135f428927a1248d71984a937ee543e
h(digest1 + digest2) is the root of this hash tree, known as the Merkle root, which must be a unique identifier of this exact tree. To check if the client-side Merkle tree is corrupt, you only need to recompute its Merkle root and compare it to the canonical Merkle root.
To pinpoint a faulty block, request the two hashes below the root in the canonical Merkle tree, and figure out which hash doesn’t match up with our client-side tree, repeat until the base is reached. Assuming there’s a single faulty block, this will let you pinpoint that block with only O(logn) comparisons (where n is the number of underlying data blocks).
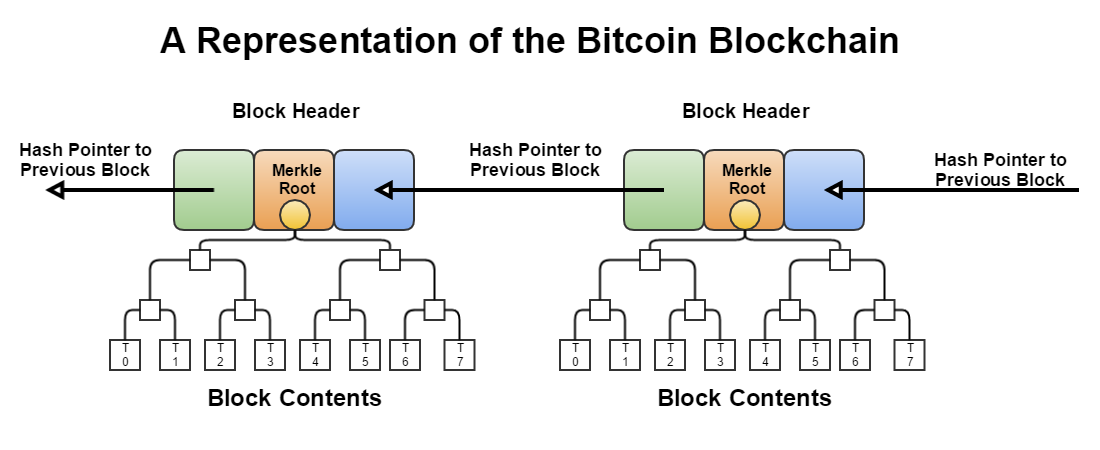
To save bandwidth, Satoshi proposes only using block headers: instead of broadcasting all transactions in the previous block, only the Merkle root is transmitted. Despite that, the blockchain size was 317 GB at last measure, still a burden for most retail machines to store.
Simplified Payment Verification
Similarly, to confirm a transaction has been accepted into a block, you only need to download the block header instead of downloading every transaction and every block. A “light client” can download just the chain of block headers: 80-byte chunks of data for each block that contain only five things:
- A hash of the previous header
- A timestamp
- A mining difficulty value
- A proof of work nonce
- A root hash for the Merkle tree containing the transactions for that block.
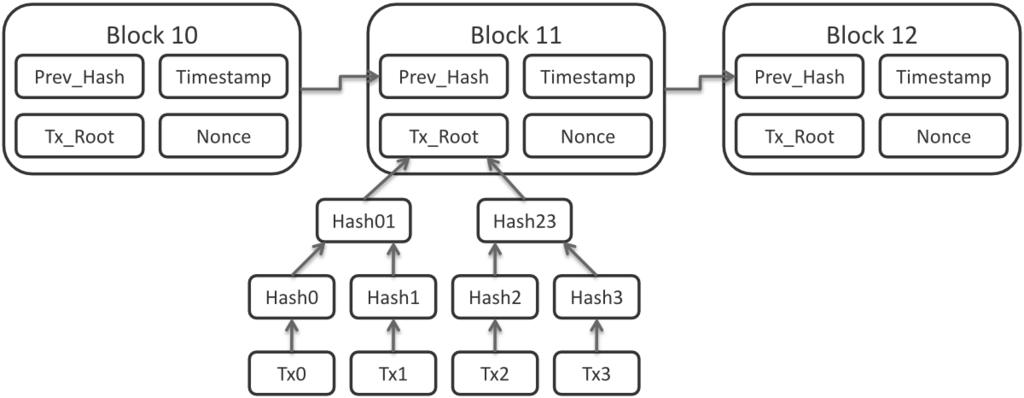 Data structure of blocks in the ledger.
Data structure of blocks in the ledger.
For example, to check Tx0, you only need to Hash0, and request Hash1 from another client’s block to get Hash01 by hashing Hash0 and Hash1. You then can then request Hash23 from the other client’s block, then hash Hash01 and Hash23 to get the Merkle root Tx_Root, and compare with the Merkle root in the block header.
This kind of inclusion proof is known as a Merkle proof, which also only requires O(logn) hashes to transmit.
Combining And Splitting Value
Combining transaction amounts will result in more efficient transfers as opposed to creating a separate transaction for every cent involved. For example, Alice transfers 10BTC to Bob, if Bob wants to transfer 2BTC to Charlie, he can set up a transaction with one input of 10BTC and two outputs of 2BTC to Charlie and 8BTC to Bob himself.
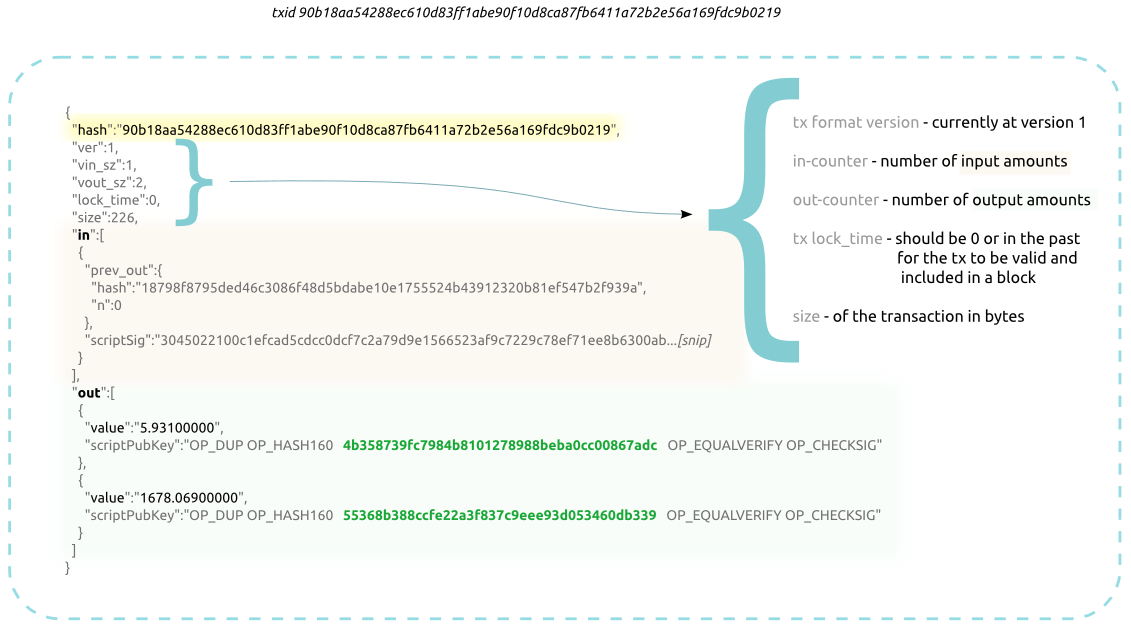
Example of a Bitcoin transaction
Privacy
A new key-pair should be used for each new transaction. For example, Alice wants to transfer 2BTC to Bob, she will set up a transaction with input of 10BTC and with two outputs of 2BTC to Bob and 8BTC to Daniel, where Charlie is her new identity so no one can link Daniel to Alice.
In practice, Bitcoin is only really private for those who take great caution to ensure their anonymity. Most Bitcoin is now traded between centralized exchanges that require ID and occasionally bank account verification by law. Also, transactions can be linked to individuals and companies through “idioms of use” (e.g transactions that spend coins from multiple inputs indicate that the inputs may have a common owner) and corroborating public transaction data with known information on owners of certain addresses.
Bitcoin’s speculation-fueled popularity put it in the spotlight of government and central banks long ago. For example, the US Department of Justice seized $1 billion in Bitcoin from the dark web marketplace Silk Road.
According to the Library of Congress, an “absolute ban” on trading or using cryptocurrencies applies in nine countries: Algeria, Bolivia, Egypt, Iraq, Morocco, Nepal, Pakistan, Vietnam, and the United Arab Emirates. An “implicit ban” applies in another 15 countries, which include Bahrain, Bangladesh, China, Colombia, the Dominican Republic, Indonesia, Kuwait, Lesotho, Lithuania, Macau, Oman, Qatar, Saudi Arabia and Taiwan.
Calculations
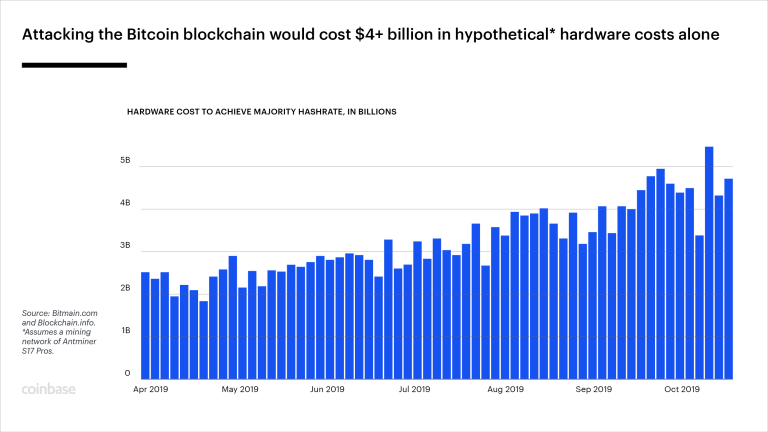
Satoshi outlines the math that makes a successful attack on the blockchain extremely unlikely. At the very least, even if someone manages to create a chain rivaling the honest one, they would not be able to create Bitcoin from thin air because honest nodes will not accept an invalid transaction. All they can do is race the honest chain to be the longest and erase their own transactions from the block they create, but again the longer the chain is, an exponentially greater amount of CPU power will be needed to catch up.
In fact, it has gotten too expensive to even try.
References
From Gwern:
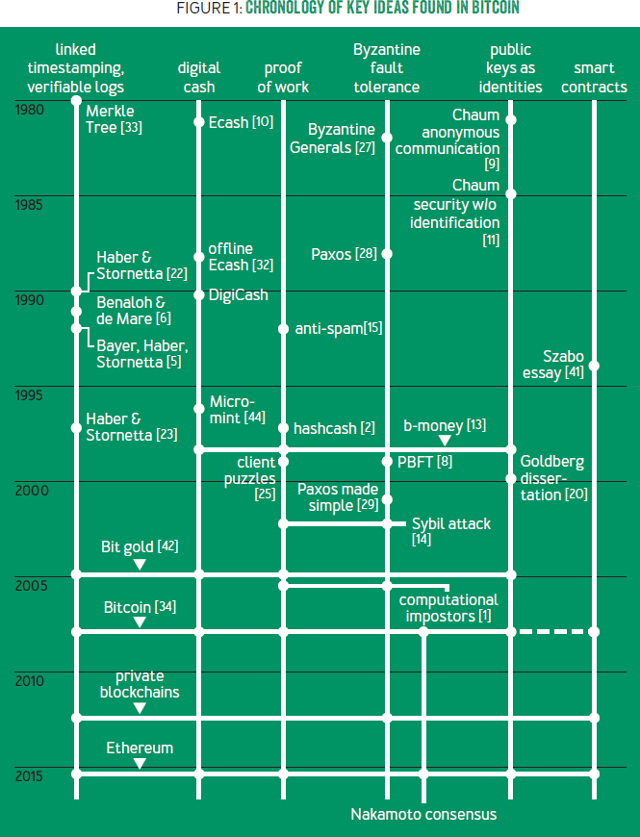
The interesting thing is that all the pieces were in place for at least 8 years before Satoshi’s publication, which was followed more than half a year later by the first public prototype. If we look at the citations in the whitepaper and others, and then order the relevant technologies by year in descending order:
- 2001: SHA-256 finalized
- 1999–present: Byzantine fault tolerance (PBFT etc.)
- 1999–present: P2P networks (excluding early networks like Usenet or FidoNet; MojoNation & BitTorrent, Napster, Gnutella, eDonkey, Freenet, i2p etc.)
- 1998: Wei Dai, B-money
- 1997: HashCash; 1998: Nick Szabo, Bit Gold; ~2000: MojoNation/BitTorrent; ~2001–2003, Karma, etc.
- 1992–1993: Proof-of-work for spam
- 1991: cryptographic timestamps
- 1980: public key cryptography
- 1979: Hash tree
This lack of novelty is part of the appeal—the fewer new parts of a cryptosystem, the less danger. All that was lacking was a Satoshi to start a Bitcoin.
Bitcoin is worse-is-better: so long as the design of the initial program is a clear expression of a solution to a specific problem, then it will take less time and effort to implement a “good” version initially (and adapt it to new situations) than it will to build a “perfect” version straight away.
More Nice Graphs
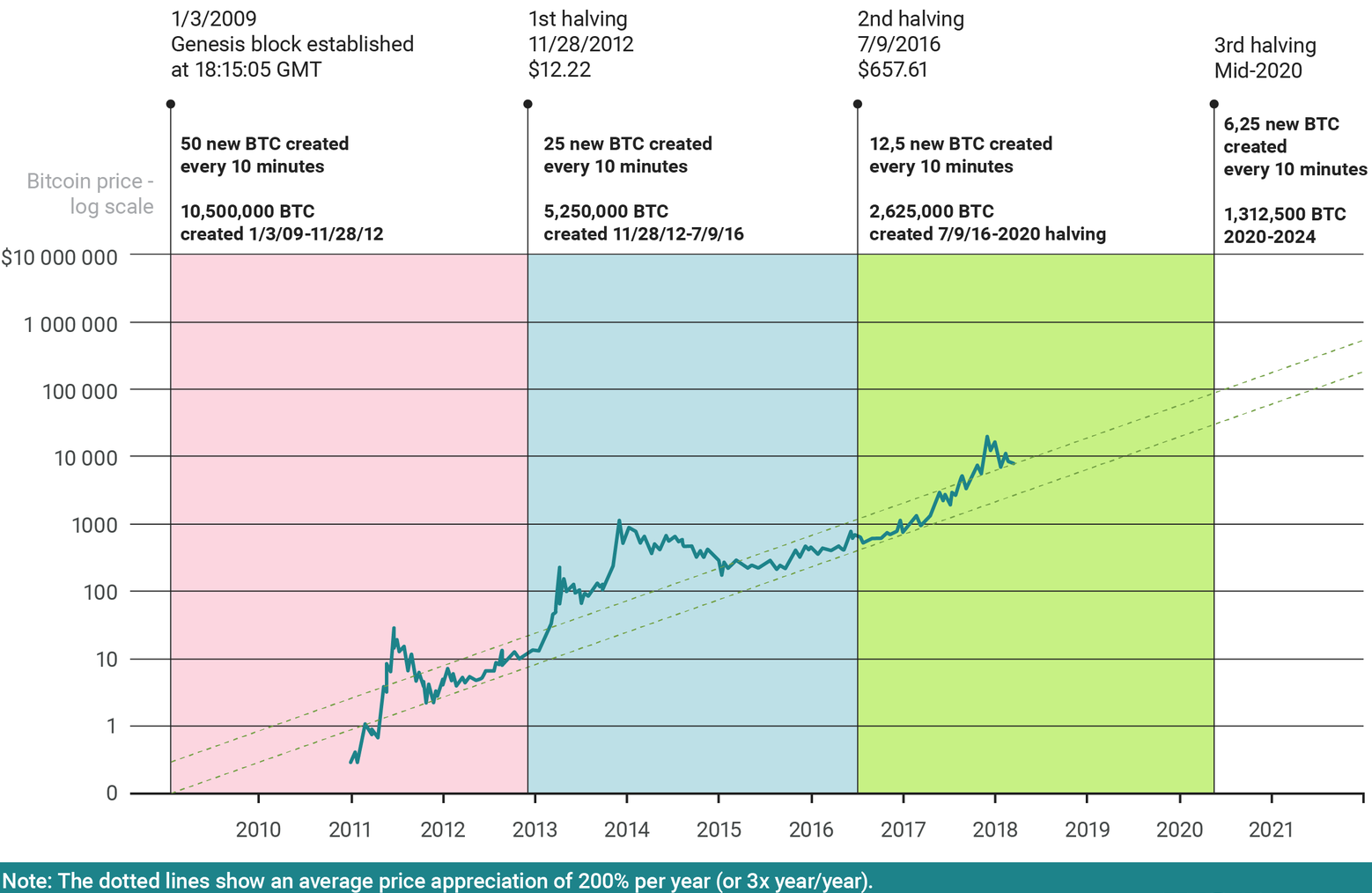
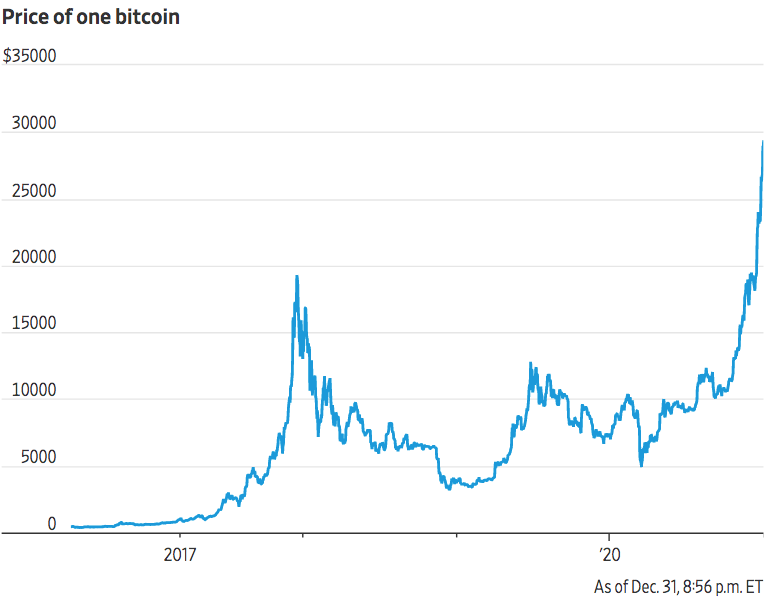
Bitcoin price showing each halving.
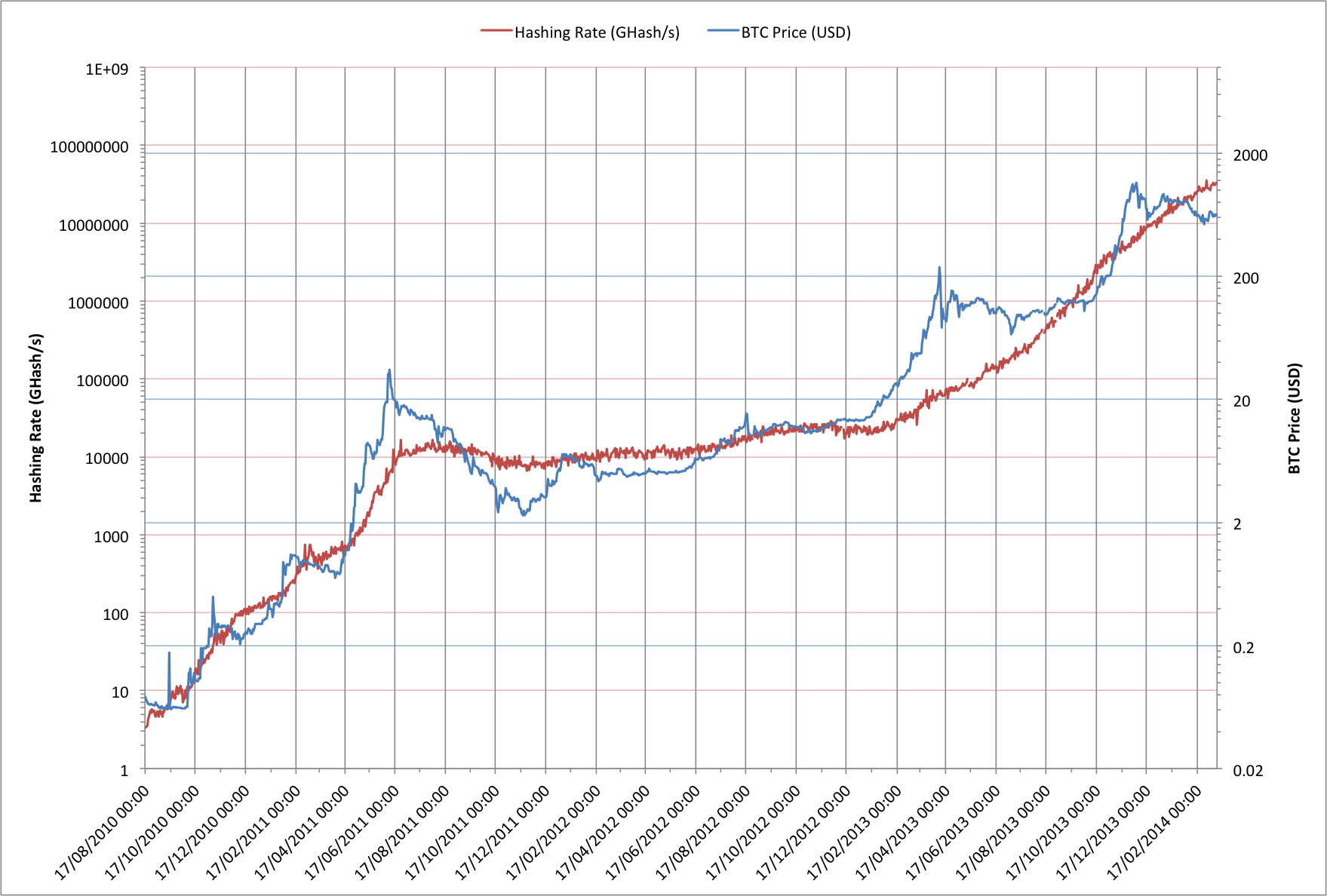
Bitcoin price against hashing rate.
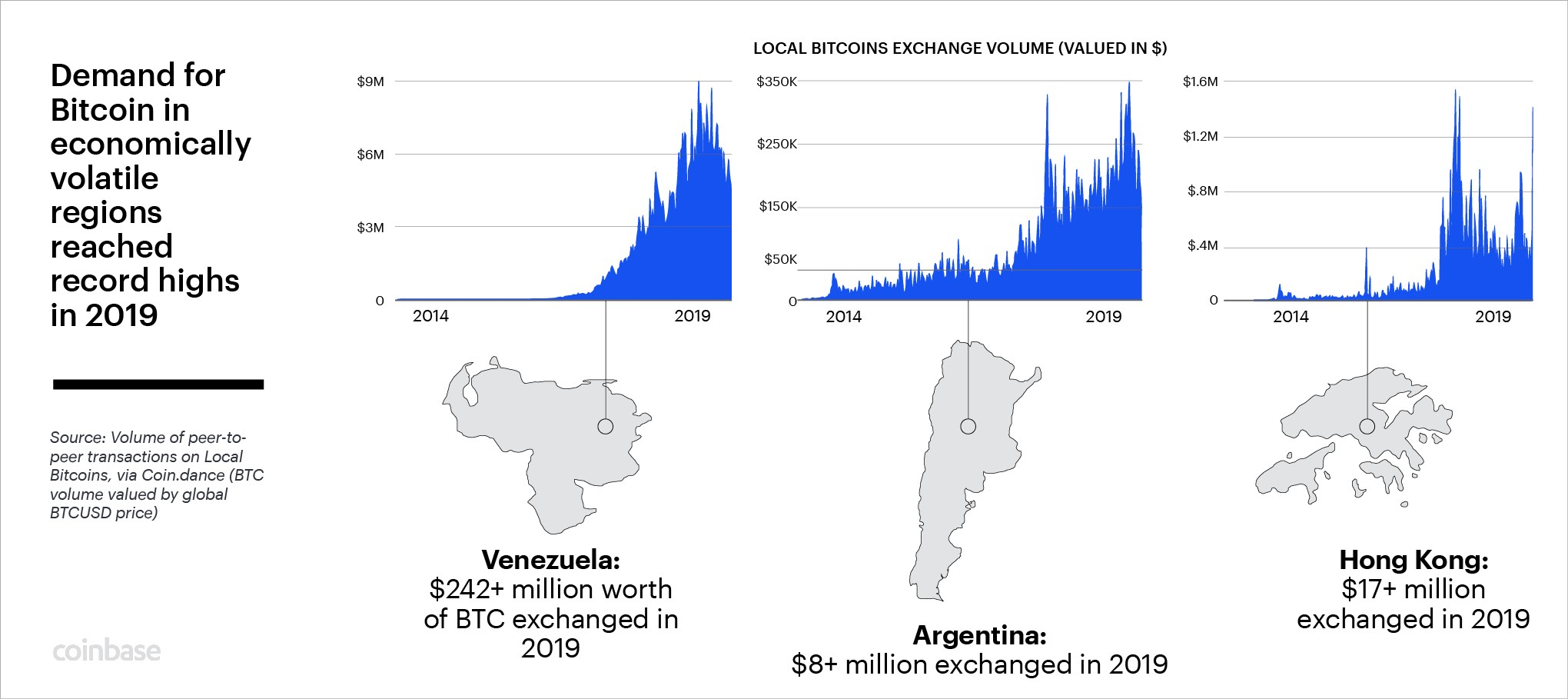
TIL Hong Kong is an economically volatile region.
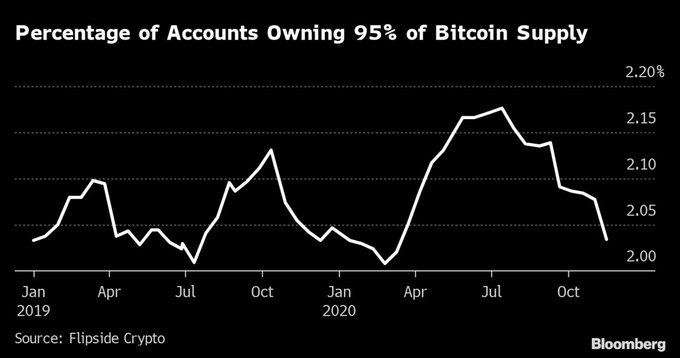
2% of accounts control 95% of bitcoin assets.
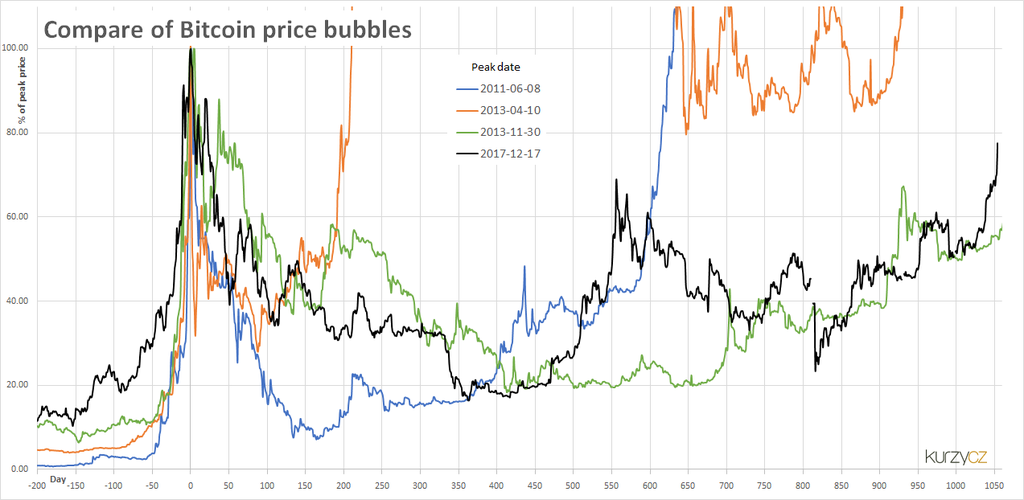
Bitcoin price bubbles in 2011, 2013 and 2017. Cryptocurrencies have long been criticised as speculative bubbles.
Additional reading
More explainers (can skip):
- Fermat’s Library’s annotated Bitcoin whitepaper
- Wikipedia article on Bitcoin
- Introduction To Cryptocurrency
- A technical introduction to Bitcoin for non-technical people
- When Bitcoin grows up
- Excellent 3Blue1Brown video on how Bitcoin (and other cryptocurrencies) work
Bitcoin/crypto:
- Nakamoto.com (2020) with contributions from all the big names.
- Bitcoin’s Guardian Angel: Inside Coinbase Billionaire Brian Armstrong’s Plan To Make Crypto Safe For All (2020)
- Stripe on Bitcoin (2014) and Ending Bitcoin Support (2018)
- In Search of the Elusive Bitcoin Billionaire (2018)
- This Is What Happens When Bitcoin Miners Take Over Your Town (2018)
- Nassim Taleb on Bitcoin (2018)
- As Traditional Payments Get Faster, What’s Left for Bitcoin? (2018)
- Why Bitcoin Will Take a Long Time to Dethrone the Dollar (2020)
- Sam Altman on Bitcoin (2013) and US Digital Currency (2018)
- Bitcoin’s Biggest Hack In History In 2010 (2019)
- A16Z Crypto Startup School
- Gwern on Bitcoin is worse is better (2011) and comment on Bitcoin as a Thielian Secret in 2011 (2020)
- Coding Bitcoin from Scratch in Rust (2020), Part 2 and Part 3
- Bitcoin’s most puzzling tradeoffs explained (2019)
- r/BadEconomics mod on Bitcoin (2020)
- Detailed report on “What’s Really Driving the Cryptocurrency Phenomenon?” (2020)
- Alex Tabarrok on Bitcoin is less secure than most people think (2019)
- Interview of Ray Dillinger and Bitcoin is a disaster (2020)
- Vitalik Buterin on mining (2014), a philosophy of blockchain validation (2017), notes on blockchain governance (2017),
- Tyler Cowen on Bitcoin will not take over the world (2020), Bitcoin volatility is a feature not a bug (2017), no longer thinks Bitcoin is a bubble (2017), Bitcoin is here to stay (2019)
Blockchain:
- Ten years in, nobody has come up with a use for blockchain (2017) and its sequel Blockchain is not only crappy technology but a bad vision for the future (2018)
- Harvard Business Review on blockchain (2017)
- Blockchain social networks (2020)
- Tyler Cowen on blockchains (2018)
- Eight Popular Blockchain Use Cases And Why They Do Not Work (2019)
- Alex Tabarrok on blockchains and the Opportunity of the Commons (2018)